What is Triangle Inequality?
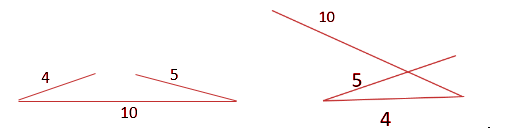
For constructing a triangle, three dimensions are required (out of 3 angles and 3 sides) with at least one of them being a side. If all of the sides of the triangle are known then a unique triangle is formed if the sum of smaller sides is more than the largest side.
Suppose if sides of the triangle are 4, 5, and 10
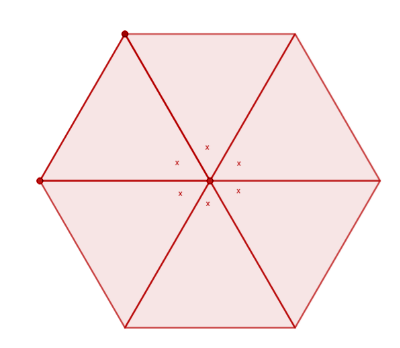
Since 6 triangles are needed to completely overlap the full circle angle and all of them have an equal share in it, x+x+x+x+x+x=360
Or, 6x=360
Or x=360/6=60 degrees
Since all of the triangles are of the same size and are equilateral, their angles are also equal. Each of the angles is 60 degrees and for the hexagon, at each vertex, there are two such angles. This means that each internal angle is 60+60 or 120 degrees.
Parallelogram, rhombus, rectangle, kite, trapezium, and square are all types of quadrilaterals. Squares are the most symmetrical quadrilateral whose all sides are equal.
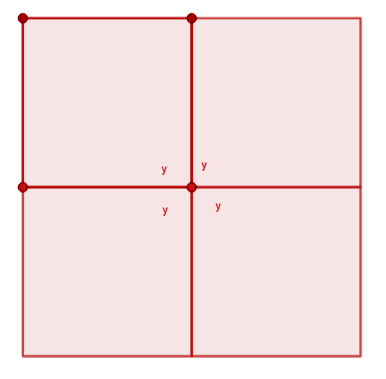
y+y+y+y=360
Or, 4y=360
Or, y=360/4=90
Constructing triangles: Unique or not?
In other cases, any side constructed first or last does not alter the shape and size of the triangle.
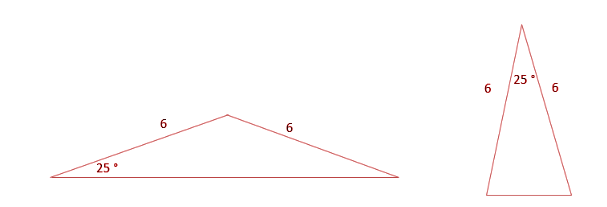
On the other hand, if two sides and one angle are given then different triangles can be constructed. For example, two sides of a triangle are 6 and one angle is 25 degrees.
Both triangles are drawn with two sides of 6 and 25 degrees only but the two figures are not the same. This means that even though the dimensions are known the order of dimensions is important. The given condition can be used to form triangles in two ways only.
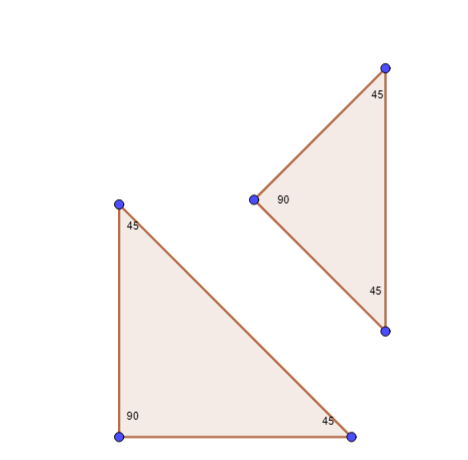
If only three angles of a triangle are known then the same shape can be drawn in different sizes. Below are two triangles made from the same dimensions given that are three angles but they are different because none of the sides were given and thus their sizes are different. With numerous sizes, we can have several triangles from the same dimensions.
If all three sides of a triangle are given (that satisfies triangle inequality) then only one triangle can be formed even though the sides may be oriented differently.