Eduki

Have you noticed the map of countries in the atlas or the world map on the globe? How can countries of huge areas be fitted on paper? What is scaling?

In the process by which the maps or any other huge objects are drawn in just one plane of the paper, the size of the objects has to be reduced to fit the paper size. The size of the plane is defined in terms of length and width. A plane may be of any shape but we are taking a standard rectangular plane for simplicity. Thus if an object has to be downsized, both its dimensions must be downsized by the same factor. 

Can the size reduction be done by subtraction?

One argument might be why don't we subtract the same amount from the dimensions of the object to fit into the paper. The argument may have been worth noticing if the area of the object changed proportionally with respect to some power of the dimensions of the figure while doing so. That is why the dimensions are multiplied/divided by a certain factor for the scaling process. 

The same applies to objects that are very small and need to be drawn in detail. Can you imagine how many times the size of the cell is magnified to get its image as shown in your science book? In such cases, the drawing must be larger than the object itself. So that all the features of the drawing can easily be seen. 

The need for scaling arose when very large or very small objects had to be drawn on one piece of paper without missing any of their intricate details. The most important requirement to scale a figure is that the shape of the original and the drawn figure must be similar otherwise there is no point in illustrating the object in a drawing. 

Comparing scaled figures

Here are two figures, decide if one may be a scaled figure of the other. 

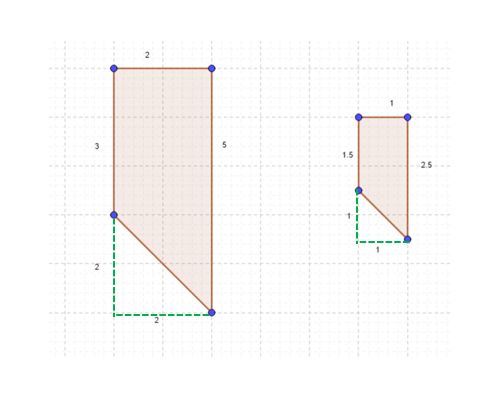
The two figures have similar shapes. All sides of the smaller figure are half of the larger shape as shown in the figure. 

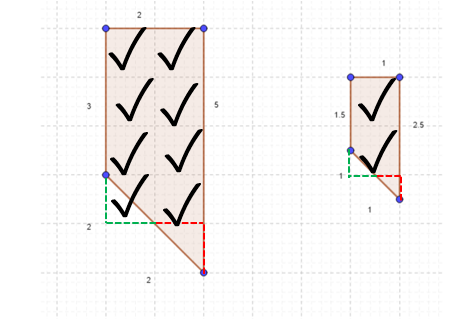
Since the dimensions of the shape on the left are double the shape on the right, the area of the larger figure is four times that of the smaller figure. We can count the squares as 2 for the smaller figure whereas the area of the larger figure is 8 square units. 

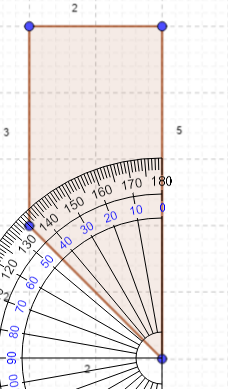
If the dimensions were scaled by 3 times the area would increase by 9 times and so on. It is also worth noting that with scaled figures if one of the sides is doubled then to maintain the same shape, all of the sides must have been doubled. Scaled figures must look the same visually thus the angles within the figures remain the same even though the sides change proportionally. The sides that are proportional to each other are known as corresponding sides of similar triangles. It can be seen in the figure that both angles measure 55 degrees and they are known as corresponding angles of similar triangles.

While measuring an angle with a protractor, one of the arms must coincide with the 0-degree horizontal line in the protractor and the vertex of the angle must be at the same position as the center of the protractor. Then it is found out in which division the other arm of the angle coincides and what is the direction of rotation between the 0-degree arm and the one being used for measurement. Here the direction of rotation is anticlockwise, thus the values in blue are noticed.