What is Rigid Transformation?
Transforming any object is the process of changing the orientation or location or size with a different mechanism for different applications. There are two types of transformations; rigid and non-rigid. Rigid transformations are those processes in which shape and size of the object gets conserved and such can be achieved when the orientation or location or both are changed. Reflection, rotation and translation are examples of rigid transformations.
Non- rigid transformations don't conserve the shape and size of the object. Dilation is one such example of non rigid transformation in which the shape remains the same but the size of the object changes.
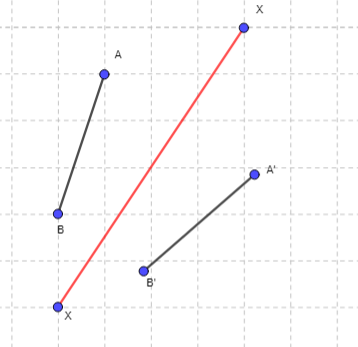
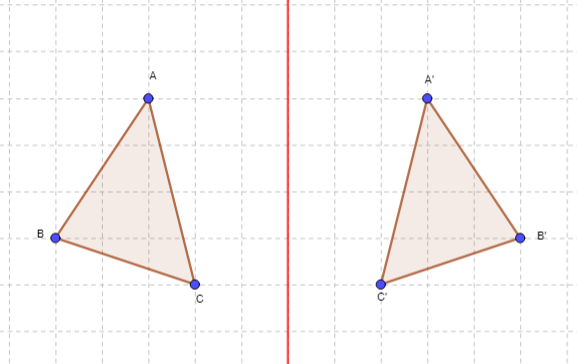
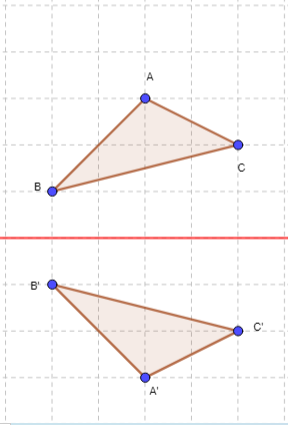
Reflecting image is dependent on the axis of reflection (its orientation and distance from the object)
The objects and images are generally differentiated on the basis of diagram labels. Images are labeled with a dash on the letters. Here are some images showing objects and their reflections. The perpendicular distance of object from the axis is same to that of the image. The sides of the object flips sides from right to left or top to bottom and vice versa.
Reflection as a medium of understanding symmetry
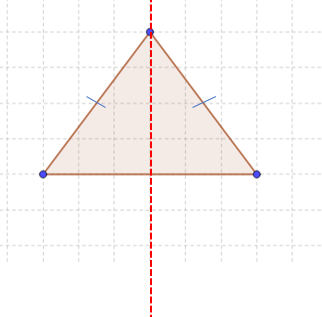
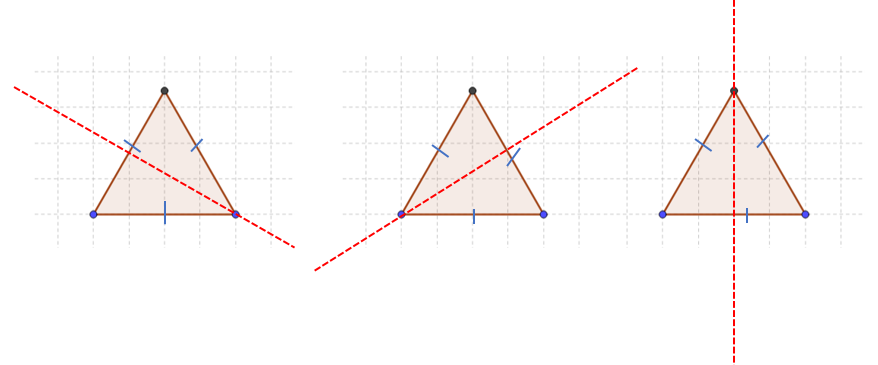
Reflections are also used as a medium to understand how much symmetric a given object is. It explains the properties of different 2D objects with line symmetry. For example, lets observe this isosceles triangle.
We can see that the left part and right part are exact copies of each other and seem flipped around the straight line shown through the middle. If we fold the part lying left of the line then the part lying on the right is completely overlapped.
If we look at an equilateral triangle, we can find three such lines that the figure is symmetric about.
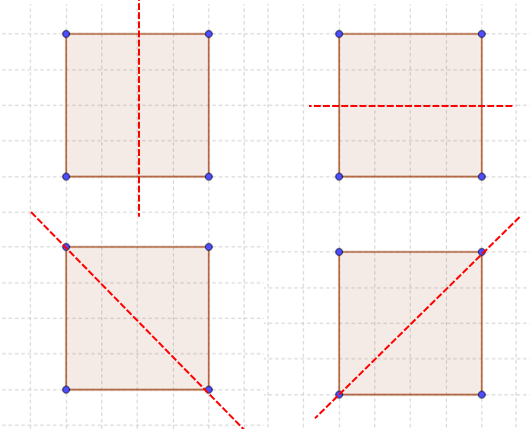
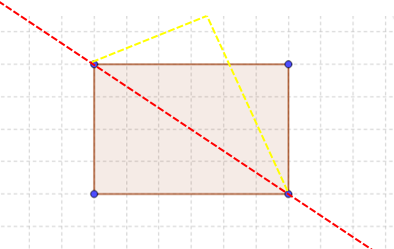
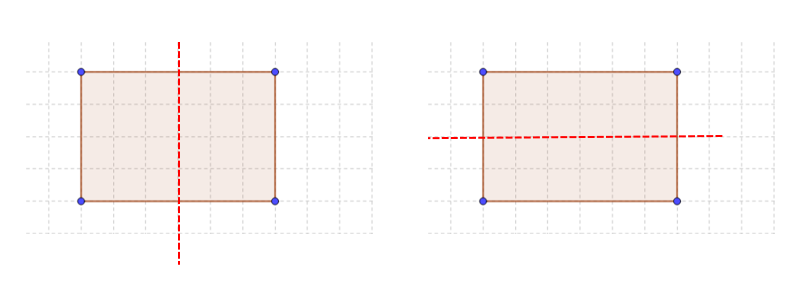
Likewise, a square has four lines of symmetry. How ever the same cant be seen with rectangles. The two lines of symmetry on the bottom two figures cant be observed in a rectangle.
Lets see what happens with a rectangle if we fold half part of it along the diagonal. The bottom part does not completely overlap with the top part. This can be realized with a rectangular sheet of paper when you may have tried making different origamis.
Thus rectangle only has two lines of symmetry; the horizontal and vertical.
If you want to know about other rigid transformations then visit the links below: