Eduki

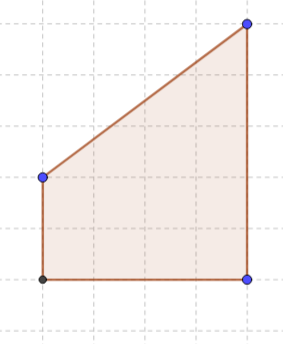
A polygon is a closed 2D plane figure that has more than 2 sides. There can't be any intersection or cross between the sides which means that the sides of a polygon can meet at a maximum of one point only. Any polygon can be decomposed into several triangles and some into rectangles as well and the areas can be found. For example, the figure given here is a trapezium whose one pair of opposite sides are parallel and the other is not. 

 

 

The given diagram is composed of a rectangle and a triangle. The same process can be used to find the area of the given trapezium as 14 square units. 

 

Multiple decompositions and composition applied on polygons

At all times a polygon can be decomposed into many squares and some triangles or simply a rectangle and triangle. The total area of all those decomposed pieces gives the area of the original piece. 

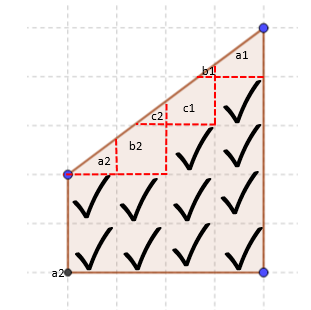
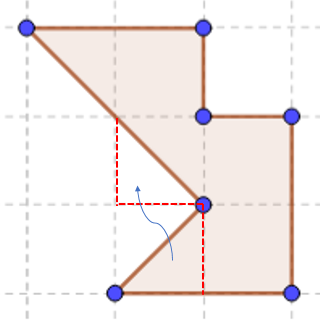
Let’s take another example in which multiple decompositions have to be done. 

Firstly the parts that make up a unit/half square are identified and replaced in those areas. Even after that, there are three half squares. 

 

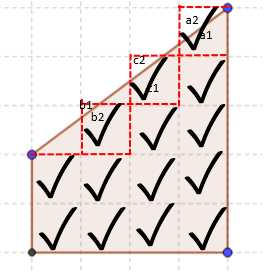
Among them, one half is replaced in the space of another half as shown in the above figure. Finally, the figure obtained is,

The total area of the figure thus is 4.5 square units. 

It is always a matter of focus on what missing fraction of the irregular part of the figure can be completed to make a full unit square or half square using the other available fractions from the same figure. The process may be done repeatedly. 

 

The area of the triangle is half of the rectangle

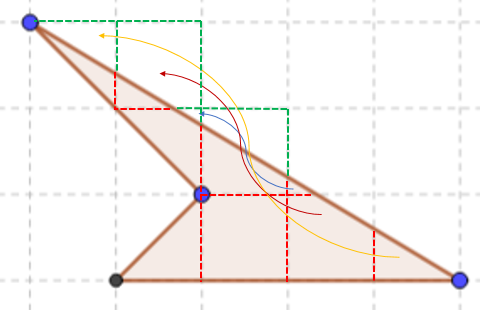
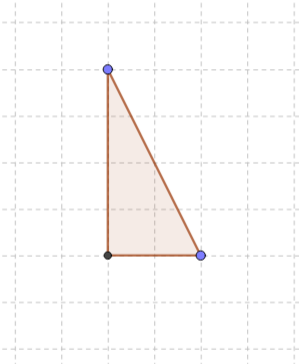
Let's examine one of the earlier figures 

The area of the triangle is half of the rectangle at the same location and dimensions

The area of the triangle was found to be 4. It is also equal to half of the area of the rectangle that can be formed in the same base with the same height. It is because of the line joining the opposite points in the rectangle dividing it into exact half. 

Area of rectangle=8 units

Area of triangle=(½) x 8=4 units

 

The area of the triangle is half of the rectangle

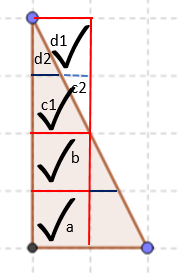
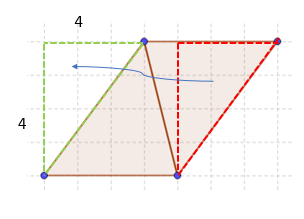
It can be seen that the two sides which were multiplied to get the rectangle area were perpendicular to each other, but the same process can be applied to other cases as well.

 

 

Here the area of the rectangle is 4 x 4= 16. 

The half of the rectangle is 8 square units. But that can't be found out by multiplying any two of the sides of the triangle. Rather it can be found by multiplying the height of the triangle with its base which is the same as the length and breadth of the rectangle. 

The base and height of the triangle are supposed to be at right angles to each other. The area is equal to half of their product. 

Area of the given triangle=(½) x 4 x 2=4 square units

 

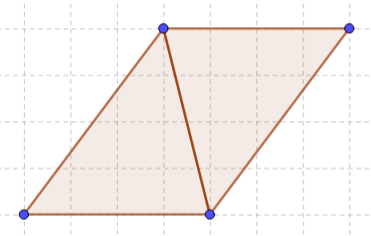
Area of parallelogram

Now let’s suppose another figure that is formed by doubling the triangle; a parallelogram

The same triangle is copied in a different orientation. In such cases, the opposite sides of the new figure are parallel to each other. According to that the area of the figure must be 16 square units. 

If the concept of decomposition is applied, we obtain the rectangle (square) of 4 by 4 size. Therefore the area of such parallelograms is equal to the product of base and height. It can also be said that the area of a parallelogram is the same as the rectangle standing on the base and enclosed within the same parallel lines as shown in the figure below. The length and breadth of such rectangle formed is the base and height of the original parallelogram respectively.

Thus, area of parallelogram= base* height