Eduki

When the letters/symbols are used in a mathematical expression along with numbers and operators, then it is an algebraic expression. Such placeholder symbols or letters are known as variables. What kind of letter or symbol we choose is totally independent of whatever quantity we are assuming, it can be any letter or symbol. If we suppose the price of an apple to be p or a, it is just for convenience and not because it represents an abbreviation of some sort. It's not written that a particular variable may be used for a particular quantity only. But the same variable cant is used to depict two different quantities in the same context. If the number of apples is denoted by “t” then it should not be used to denote the number of oranges or any other fruit in the same context. 

we can understand that expressions are made up of two types of entities; variables and constants. Variables are those that don't show/represent one particular value and constants are those entities that represent one particular quantity. Even though the variables don't represent one particular quantity, they represent some quantity. 

One notion may be set up in your mind now that whenever letters are seen in an expression, they are variables. There are certain symbols particularly greek that are used to represent constant values such as π, prominent in formulae related to curved surfaces or circles. It represents 3.14 and is always equal to that value in whatever context it may be used.  

Expression as a quantity

Expressions either numerical or algebraic, carry some value to themselves. It may not always be one particular value but they represent some quantity (may it be known or unknown). In the case of algebraic expression, we must substitute the variable with a particular value to find the corresponding value of the expression. 

It's not mandatory that some statement or operation in algebra can always be expressed through a combination of variables and constants. It can also be done through tables or graphs. Expressions can be transformed into tables or graphs by finding the potential values of the variable and comparing that with the values of the expression.

Parts of expressions

Since an expression corresponds to some quantity, the parts of the expression that form itself are also quantities. Each part can be identified as a separate quantity. For example: if the cost of 3 pens and 5 notebooks is 3𝑥 + 5y then 𝑥 is the price of one pen or unit price of pen and y is the price of one notebook or unit price of the notebook. 3x is the total price of all pens and 5y is the total price of all notebooks. The parts of expressions are separated by an operator. Operators can be addition “+”, subtraction “-”, multiplication “*” or “x”, division “÷” or “/”, the root “√” etc. Sometimes parts of an expression may not seem to use any operators, it is done in the cases of multiplication.

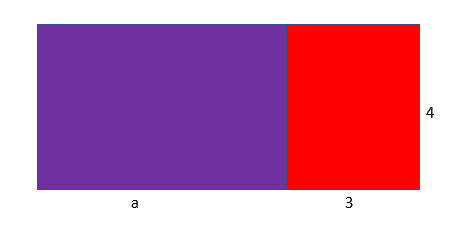
The area of a purple rectangle is 4 x a because the dimensions of the rectangle are 4 units width and “a” length; The area of a red rectangle is 4 x 3 or 12 because the red rectangle is 4 units wide and 3 units long. The total area in the figure is 4a +12 if we add both the area of the rectangles. If we look at the dimensions of the whole rectangle (red + purple) we find that it is a+3 units long and 4 units wide. Thus the area of the whole rectangle is 4 x (a+3). Both 4 x (a+3) and 4a +12 must be equal. The parentheses are used in place of the multiplication operator. If we want to know the real value of the area of the whole rectangle, then the value of a must be replaced. Let's suppose that the value of a is 5 units. Then the value of the expression is 4 x (5+3) or 32. The value is the same even if we put a=5 in 4a+12. 

Now let's observe some techniques to get equivalent expressions. If “𝑥” blue t-shirts, “y” red t-shirts, and “z” yellow t-shirts are bought then the total number of t-shirts can be expressed as 𝑥 + y + z. If a blue t-shirt cost 3 dollars, a red one cost 2.5 dollars and a yellow one costs 2 dollars, the total cost of buying a blue T-shirt is 3𝑥, for red it's 2.5y and for yellow its 2z dollars. Thus the total cost of all the t-shirts is 3𝑥+2.5y+2z dollars. 

The order of operations

Expressions are used because they simplify complex statements into short forms full of symbols. And the meaning of the symbols isn't different in different circumstances apart from the variables. While finding the algebraic expression from a statement, the PEMDAS rule is followed in which the operation of division/multiplication comes ahead of addition/subtraction. PEMDAS is an acronym for parenthesis, exponents, multiplication, division, addition, and subtraction. For example, if we are to find “5 less than 7 times a number” then it is 7𝑥-5 and not 7(𝑥-5). Here “less” is used for subtraction operations whereas “times” is used to represent multiplication. Since multiplication has to be done first, we focus on it first. It says 7 has to be multiplied by a number that isn't known. Thus a variable is represented by the letter 𝑥. Only after the multiplication, the subtraction operation is expressed. 

Here any letter or symbol can be used in place of x unless it means any other thing already. 

If we have to find out a number that is 5 lesser than 7 times 6 then we just plug in the value of the variable in the expression.

7*6-5=37

Expressions always tell something about a situation mathematically. The operators used in expressions are a direct translation of the meaning that a statement provides. For example, if an expression says double the amount of an unknown number, we first need a placeholder variable for the number and then multiply that with 2. If an expression says that the amount of food cooked is 50 kg less than yesterday and the amount of yesterday isn't known then we need a placeholder variable to assume the unknown amount of food and subtract 50 from it. The expression would look something like 2f-50.