Volume of cylinders

Let's start with a cylinder. It is an object formed by stacking multiple circles of the same radii one on top of the other.

Since the formula for finding the volume is base area times height and the base is circular here. 

Base area= area of circle= πr2

Volume= Base area x height = πr2 h

The surface area of the cylinders

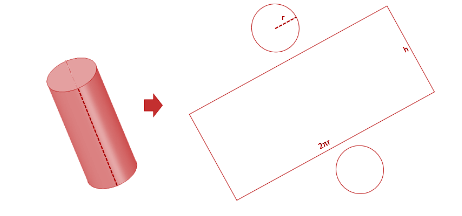
Finding the surface area of the cylinder is a little bit tricky. With polyhedra, it was easy because all of the shapes were flat and we were known to find one or more ways of finding the areas of the 2D objects constructed on a flat surface. When it comes to the curved surface that is formed that joins the two circles in the base. What we do is cut the curved surface parallel to the axis such that we get a rectangle and two circles at the two ends.   

The thing that has to be noticed is that the length of the rectangle is equal to the perimeter of the circle at the base because the whole curved surface is untwined along the circumference. The width of the rectangle is equal to the height of the cylinder. Thus now we have one rectangle with its precise dimensions and two circles. All of their areas can be easily found using the formulae learned before. 

Total surface area = area of two circles + area of the rectangle

=2πr2 + 2πrh

Surface area of cones

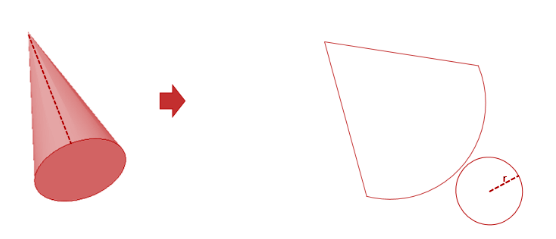
Let's have a look at the cone. A cone to the cylinder is similar to what a pyramid is to a prism. The area of the circle at the base goes on decreasing as the height of the cone increases.

 

 

The curved surface formed is such that when it is untwined just like the cylinder, we get shape as shown in the figure. 

 

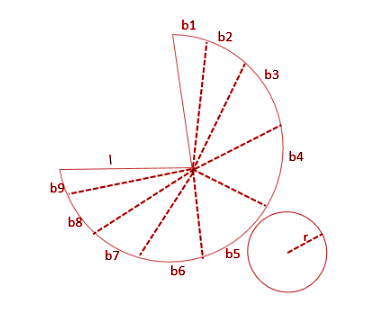
The curved surface can be divided into small triangles such that the bases are drawn in the arc-shaped part. The heights of all triangles are equal to the slant length (l) of the cone. If there are many such divisions made such that the curved part is as straight as in a triangle. 

Let the bases of all the divisions be b1, b2, b3, b4, b5, ……….. to n parts

Area of triangle = ½ x base x height 

Area of all triangles= ½ x (b1+b2+b3+b4+......+bn) x l

Here l is the slant height of the cone and must not be confused with the actual height of the cone. The slant height is measured along the curved surface of the cone that is a bit slanted with the vertical. 

Regardless of what the values of bases are, their sum must be equal to the circumference of the base circle. 

b1+b2+b3+b4+......+bn=2πr

Total area of the curved surface=½ x (b1+b2+b3+b4+......+bn) x l

=½ x 2πr x l

∴ Curved surface area of the cone = πrl

Apart from the curved part, there is one circle= πr2

Total surface area= πrl + πr2

=πr(l+r)

Volume of cones

The volume of the cone is found to be ⅓ of the total volume of the cylinder with the same radius and height. It can be verified experimentally by taking a cone and a cylinder of similar dimensions. If a liquid is filled in the cone and then emptied into the cylinder, it requires liquids in three cones to fill the cylinder up to the brim. 

Volume of cone=⅓ πr2h