Eduki

Adjacent angles

Two angles can also be related with different relationships. 

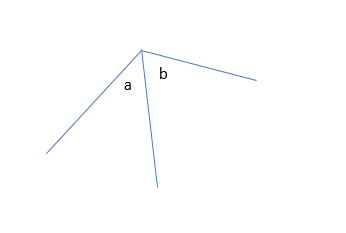
For example, if two angles share one arm, then they are known as adjacent angles. For example, in the given figure a and b are adjacent to each other. 

 

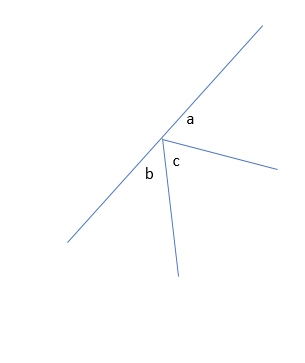
If for a pair of adjacent angles, the other arms are part of the same straight line then they are known as supplementary angles. The supplementary angles don't need to be in pairs, but all of the angles must be formed within the same straight line and share the same vertex. The sum of supplementary angles is 180 degrees. For example in the given figure: a, b and c are supplementary. 

 

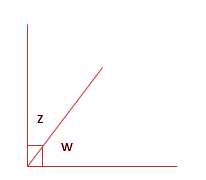
If angles share arms and are formed within a right angle, then the angles are said to be complementary. The sum of complementary angles is 90 degrees. For example, z and w are complementary to each other. 

 

If we know that two angles are complementary and one of them is 58 degrees then by the properties of complementary angles we know that their sum is 90 degrees. 

The unknown angle= 90-58=22 degrees

Vertically opposite angles

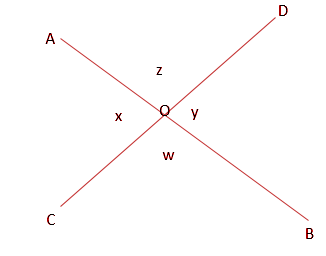
If two angles are formed with the intersection of two straight lines and angles are opposite sides of each other then they are called vertical angles or vertically opposite angles. Vertical angles are equal to each other. 

 

In the figure, ∠AOC and ∠BOD are vertically opposite to each other. And so are pair ∠AOD and ∠BOC. 

Using these relationships we can find several unknown angles which may not be directly given. 

For example, if we know that ∠AOC is 70, then we automatically know that ∠BOD is also 70. 

Also since AB is a straight line and there are just two angles formed within the straight line; ∠AOC and ∠COB. They must add up to make 180 degrees. 

 

∠AOC + ∠COB =180

Or, 70 + ∠COB =180

Or, ∠COB= 180-70=110

 Since 

∠BOC is 110, ∠AOD must also be 110.