Eduki

After getting familiar with proportional relationships, we will look at one of its representations other than a table and a double number line. It is a generalized form which represents all proportional relationships in a given case - equation! You might need to be familiar with the idea of some algebra for this, but we will walk you through the process, nonetheless. 

Given is a table that shows the amount of red and yellow paints in parts needed to make a shade of orange paint.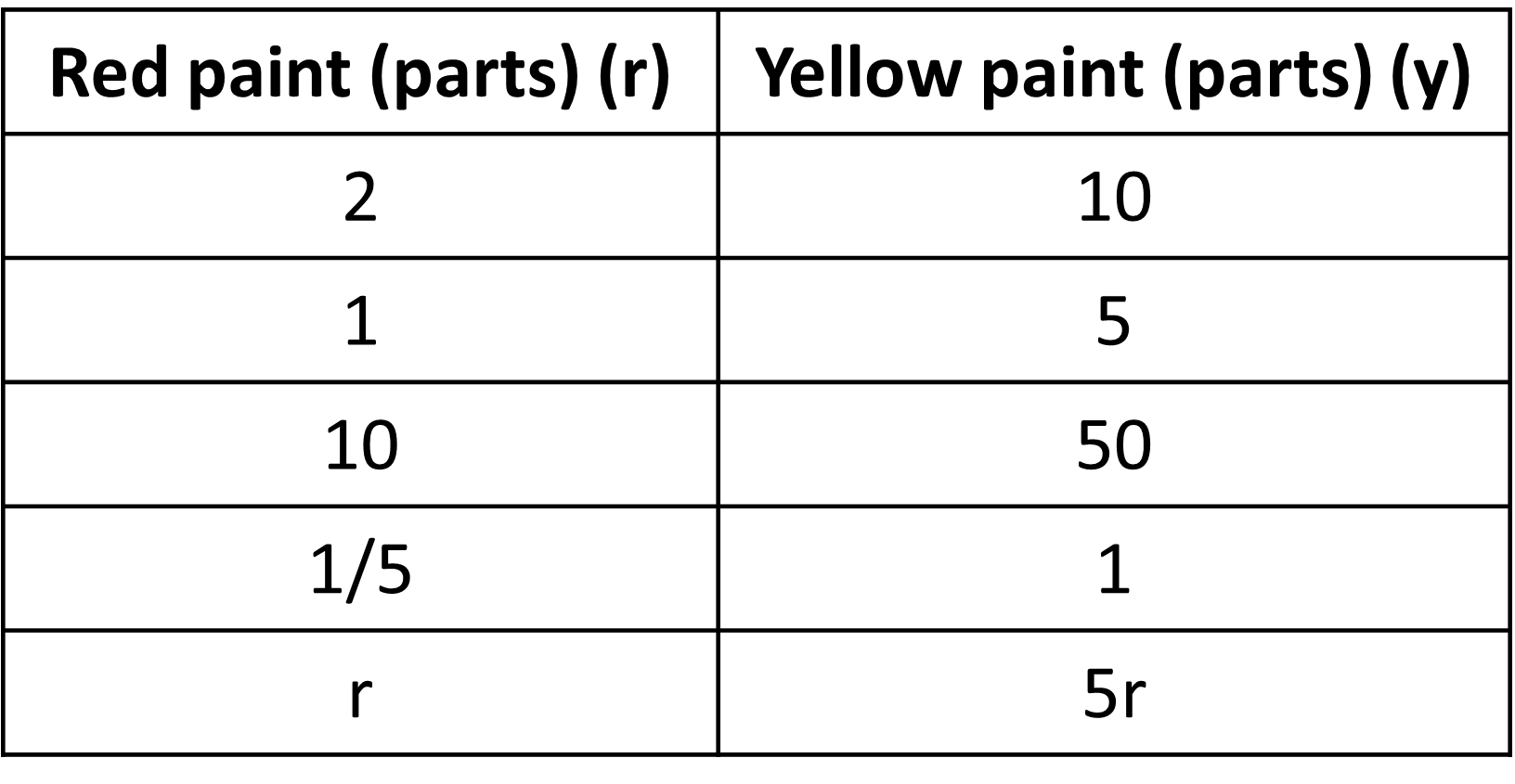

The amount of red and yellow paint is proportional to each other, so they are all equivalent ratios. Also, we know that we can get one value from the other by multiplying by the same constant, the constant of proportionality. Here, to get the amount of yellow, we can multiply the amount of red by 5 for all cases. This helps us in coming to a general conclusion. For 1 part of red, you need 5 x 1 parts of yellow. For r parts of red, you need 5 x r parts of yellow, as seen in the last row. 

Yellow paint can be denoted by y, so we can write it as y = 5r. 

In this case of the equation, we have taken the unit rate where we first find how much is needed for 1 part red. The statement to be used here is that yellow is proportional to red, implying that the amount of yellow is dependent on red, since 5 times red gives yellow. Since we use 5 for all cases and this is the unit rate as well, this is the constant of proportionality. This is one advantage of using the equation as it shows the constant as well. 

But here, the idea of proportionality is interchangeable since we could determine the amount of red from yellow as well. Meaning red is proportional to yellow. So, we need to write the equation in a way that shows us how we get red when we have yellow. We can easily do that by simply using symbolic transformation on the equation.

y = 5r

Dividing by 5 on both sides,

y/5 = r

r = y/5 

r = ⅕ x y

We are told that the constant of proportionality has to be the number of the coefficient given, which is 1/5 here, which aligns with our previous idea of constants being reciprocals. How about the idea of unit rates? How much red paint is needed for 1 part yellow? We see that it is ⅕, so the equation aligns with all our previous ideas!

Thus, an equation is useful since it helps us understand the idea of two constants of proportionality as we can easily interchange between the two and align with all the ideas from before as well. 

---

To generalize, when two quantities x and y are in a proportional relationship, we can write the equation y = kx and say, “y is proportional to x.” (This is because we find y from the value of x given, implying that y is dependent on x). In this case, the number k is the corresponding constant of proportionality (Assuming that k is the unit rate, meaning the value of y when value of x is 1. You can find this by replacing the value of x as 1, which gives us y = k.). We can also write the equation x = 1/k y and say, “x is proportional to y.” In this case, the number 1/k is the corresponding constant of proportionality. Each one can be useful depending on the information we have and the quantity we are trying to figure out.

Using equation to find missing values

Finally, equations are also a pretty good way to find missing values when one value is given, which helps us find multiple values to fill in the table. From the previous case, we know the equation for red and yellow paint is r = ⅕ x y. No, if we know the amount of yellow paint, say 150 parts, which is a pretty big number, we can use the equation to find the amount of red needed. In previous cases, we would have used a number line diagram or tape diagrams, which would have been a hassle since 150 is a big number or draw. 

Using equation r = ⅕ x y, we can simply replace the value of y and find r:

r = ⅕ x 150 = 30

So, 150 parts yellow requires 30 parts red to make the same shade of orange.

---

To begin with what ratios are, visit our other post: What do we mean by Ratio?

To understand the equivalent ratios, visit our other post: What are equivalent ratios and how exactly do we find them?

For double number line, visit our other post: Do we need double number line in ratio?

To understand proportional relationships, visit our other post: Ratio to proportional relationship: How do they connect?