Eduki

When we have a prism we must decide what its base is. Normally we associate base with the face on which the figure sits but it is the area that is constant throughout the prism while cutting at any section of the object. It can only happen in this object if the cut is made parallel to the triangular face. Thus the triangle is the base. For finding the volume we must find the base area and multiply it by height. We have several methods of finding the area of a triangle. 

It can be found by halving the product of the base and height of the triangle if the base and height are known. 

If we know that the triangle is right-angled then the base and height are the two perpendicular sides of the triangle. 

If we know that the triangle is equilateral (all three sides are equal to each other), then it is equal to (√3/4) times the square of the side. 

If there was a quadrilateral in place of the triangle, then the formula for finding the area of the respective quadrilateral is used. 

For example for a rectangle base, area= length x breadth

For a square base, area= length2

In more of the less symmetrical quadrilaterals, it is wiser to use the decomposition concept to break down the shape of the base and find its area. 

The volume of the pyramid

For finding the volume of the pyramid, there are several formulae derived based on fractional volume concerning the prism of a similar base. In normal cases, it is found that the volume of the pyramid is ⅓ times the volume of the prism of the same base and height.

The surface area of the prism and pyramid

In the case of surface area, we find how many faces there are in the object, then find their areas then add them all together. If only the lateral surface area is asked then we must not add the area of the face that acts as the base. Two bases are parallel to each other in a right prism while there is just one base in a pyramid. The faces other than the base are rectangles in a prism and triangles in a pyramid. The number of rectangles and triangles depends upon the number of sides in the base. The lateral surface area for a prism consists of the area of all rectangles except the base (if the base is also rectangular) while for a pyramid, LSA consists of the area of all triangles except the base (if the base is also triangular). 

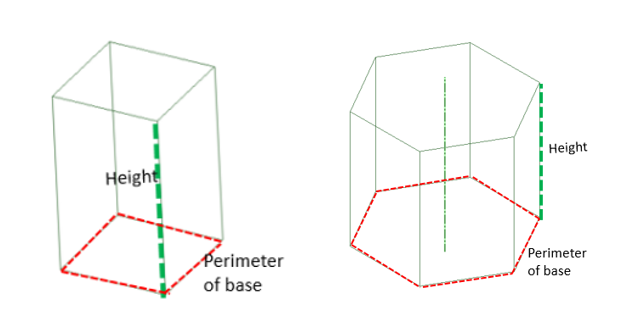
The general formula for both the lateral and total surface areas of the prism is

Lateral surface area= perimeter of the base x height of the prism

Total surface area = perimeter of the base x height of prism + 2 x base area

 

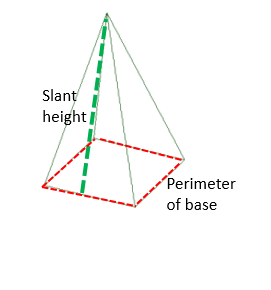
The general formula for both the lateral and total surface areas of the pyramid with a regular base is:

Lateral surface area= (½) x perimeter of the base x slant height of the pyramid

Total surface area = (½) x perimeter of the base x height of prism + base area

The slant height is the height of the respective triangle in the triangular face. 

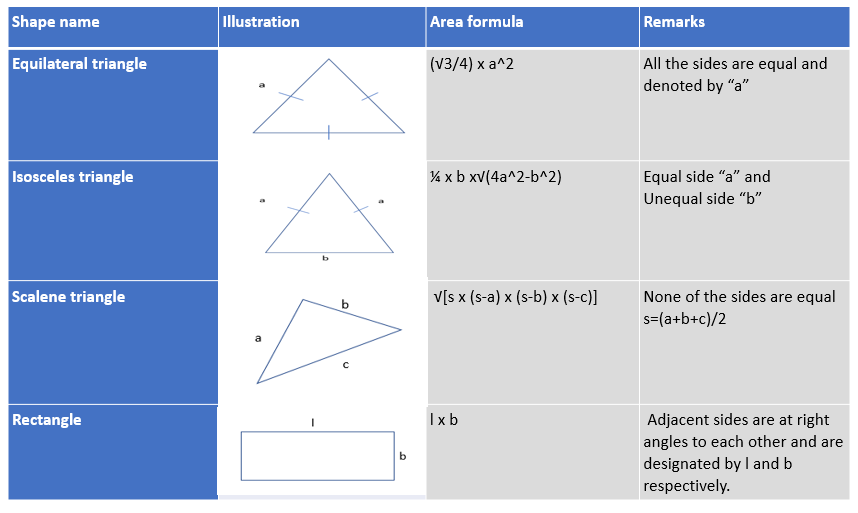
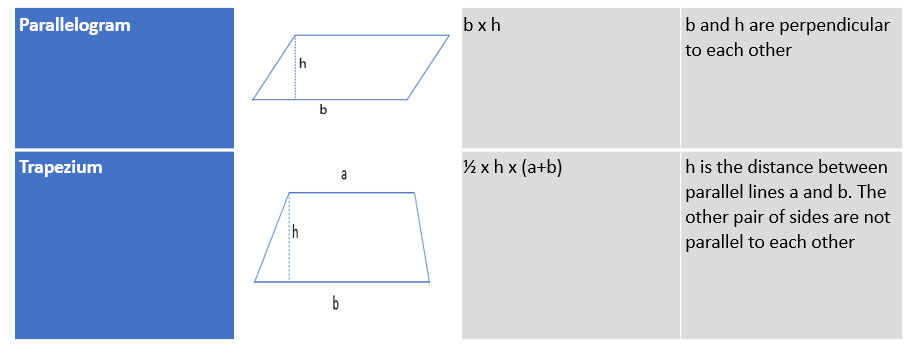
The area of the base of different shapes usually found in prisms and pyramids are: