Rotation and translation
Rotation is also known as turning. It is the process in which the orientation of the object is changed with respect to a fixed point by some angular displacement. The fixed point is known as the center and the angular displacement is expressed in terms of degrees along with the direction of rotation. For convention, anticlockwise direction is taken as positive whereas clockwise direction is taken as negative. and these angles are inverses of each other as well. For example turning 60 degree clockwise is the same as 300 degree anticlockwise. i.e. -60 is same as +300. As we can see the sum of the magnitudes of both the angles makes 360 degrees. Here are some figures of objects being rotated.
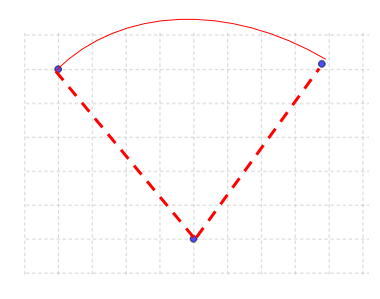
We have a triangle ABC that is rotated about the center (where the two red lines meet) clockwise 45 degrees. The rotation angle is shown for one point A only. The detailed rotation of other points are shown in the next diagram.
Each of the three points and their rotation are shown in different colors in the following figure. All of the rotations measure 45 degree clockwise because the object is on the left and its image is on the right thus to achieve we need clockwise rotation. The center is the point where all the radii of the arcs meet.
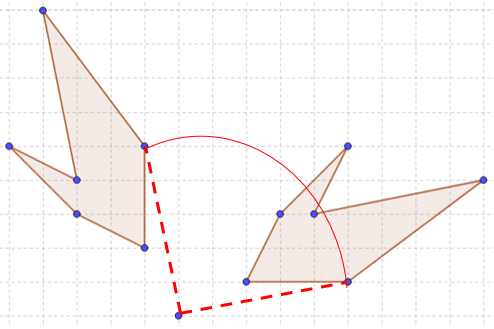
Other examples of rotation are shown in the different figures below.
Rotation as a medium of understanding symmetry
Rotation is also a medium used to explain the symmetry of a 2D shape. we all know that the full circle angle is 360 degrees and any object that rotates 360 degree about its center will return back to its original position. But there are certain shapes that return to their original position prior to 360 degrees. For example, a square gets to its initial position at 90, 180, 270, and ultimately 360 degrees rotation. A rectangle gets to its original position at 180 and 360 degrees. Thus square has 4 angles of symmetry and rectangle has 2. Each shape however irregular it may be, it has at least one angle of symmetry which is 360 degrees.
Translation
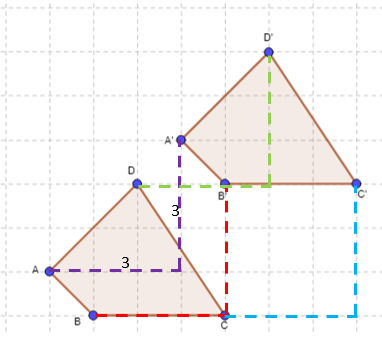
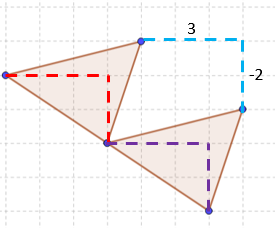
is also known as sliding and involves the process of changing the location of the object. It is generally denoted by a vector. Normally vector represents some horizontal displacement and some vertical displacement. The sign convention works in the same way as the cartesian plane does. If a vector is represented by (2, -6) then it means 2 positions to the right and 6 positions downwards. An object transformed by the vector will shift in that direction. A vector can be shown in a graph with an arrow such that the tail of the arrow is the starting point and the tip of the arrow is the ending point. The sequence of horizontal and vertical displacements to reach the ending point from starting point is given by the components of the vector. In translation, the orientation of the object remains the same unlike the other two types of rigid transformations. Some of the examples of translations are shown in the figure.
If you want to know what rigid transformations are, then visit the link below: