Eduki

The reference point taken here is the origin which acts as a universal reference but the reference point can be taken anywhere on the cartesian plane. 

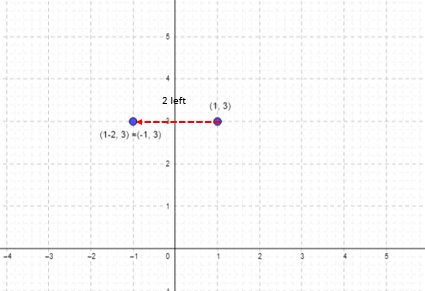
For example, what is the coordinate of the point that lies 2 units left of (1, 3)

A point 2 units to the left of (1, 3) is (1-2, 3)= (-1, 3) 

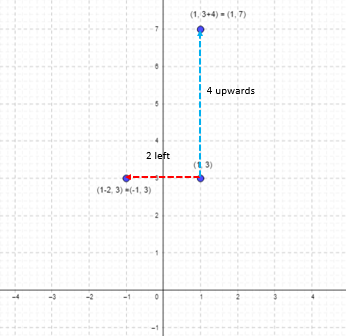
What are the coordinates of the point 4 units upwards of (1, 3)

A point 4 units upwards of (1, 3) is (1, 3+4)= (1, 7)

Now what are the coordinates of the point that lies 2 units to the left and 4 units upwards from (1, 3)

Different shapes can be defined using coordinates. For example, a 4 by 2 size rectangle has to be drawn with (-2, 3) as one of the vertices. The rectangle can be oriented horizontally or vertically. The three remaining vertices can lie on either left-top or right-top or left-bottom or right-bottom direction from (-2, 3). One of the possible options is the left-top direction. 

 

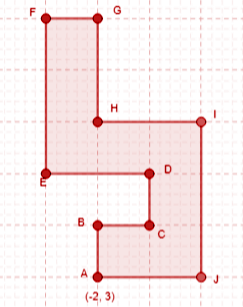
The reference point taken in the given nonagon (9-sided polygon) is A (-2, 3) which is one of its vertices as well. 

Here B is 1 unit upwards of that so the y coordinate is changed as (-2, 3+1)=(-2, 4). 

C is 1 unit to the right of B. So only the x coordinate is changed in that of B as (-2+1, 4)= (-1, 4). 

D is 1 unit upwards from C so again only the y coordinate is changed from C as (-1, 4+1)=(-1, 5).

E is 2 units to the left of D so only the x coordinate changes as (-1-2, 5)=(-3, 5)

F is 3 units upwards of E so only the y coordinate changes as (-3, 5+3)=(-3, 8)

G is 1 unit to the right of F so only the x coordinate changes as (-3+1, 8) = (-2, 8)

H is 2 units downwards of G so only the y coordinate changes as (-2, 8-2)= (-2, 6)

I is 2 units to the right of H so only the x coordinate changes as (-2+2, 6) = (0, 6)

J is 3 units downwards to I so only the y coordinate changes as (0, 6-3) =(0, 3)

 

The same results can be obtained by moving from A to J, I, H, G, F, E, D, C, and then B.