Eduki

Now that we are familiar (and maybe even experts!) with the idea of proportional relationships, let's look at examples or situations where relationships might not be proportional and how they are different from proportional ones.  

Given are two tables showing different prices for hot chocolate at two different cafes. 

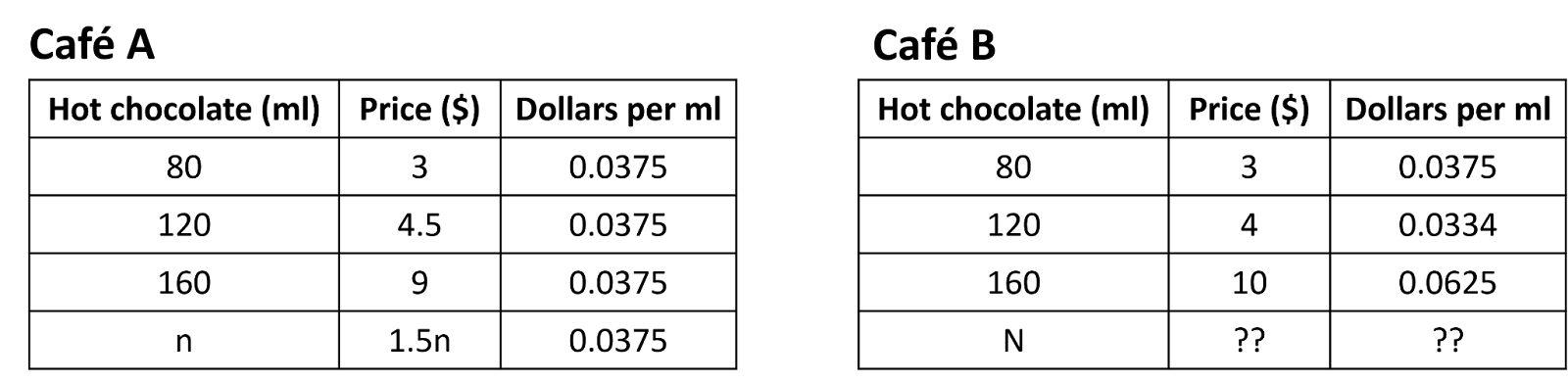
In the case of Cafe A, we see that hot chocolate costs $0.0375 per ml no matter which size we buy. If this continues, we can say that there is a proportional relationship between drink size and its price. With the help of this unit rate, we can write an equation for this as p = 0.0375s, where 's' is the size in ml and 'p' is the price of drink in dollars. Note that if even one drink size on the menu does not have the same unit rate, the whole situation will not be proportional. Since we are considering only the value given in the table, we will assume it is proportional and applicable for all sizes. The equation applies to all cases; hence it ensures that the relationship is proportional.

Moving on to Cafe B, the cost per ml is different for each size of drink mentioned. One equation cannot generalize this situation and the different unit rates mean that the relationship between drink size and price is definitely not proportional.

In general, two quantities in a proportional relationship will always have the same quotient, which are the two unit rates or constants of proportionality. We know that this means that they have a proportional relationship. But how do we express this and check for it?

Let’s look at Cafe A’s table again, this time with a slight change.

The unit rates (one of the unit rates) can be found by dividing the price by the amount of hot chocolate as seen in the third column. This gives us the same value in each case here. 

We can write this as p/s = 0.0375 which can be converted into our original equation of p = 0.0375s and the other form as well. So, if the amount of hot chocolate and its price are always proportional, then the value of p/s will also always be the same. We know this value to be the constant of proportionality or the unit rate. Note that s cannot be 0. 

So, to generalize, if y/x is always equal to one number, k, then y is proportional to x. 

y/x = k or y = kx

If you have a table with x values and an equation, you can easily find y. After this, find value for y/x in all cases. If they all are the same, then y and x are proportional!

Proportional or not?

Using the equations given, let’s fill out the value for y in each table as follows and then find the value for y/x as well.

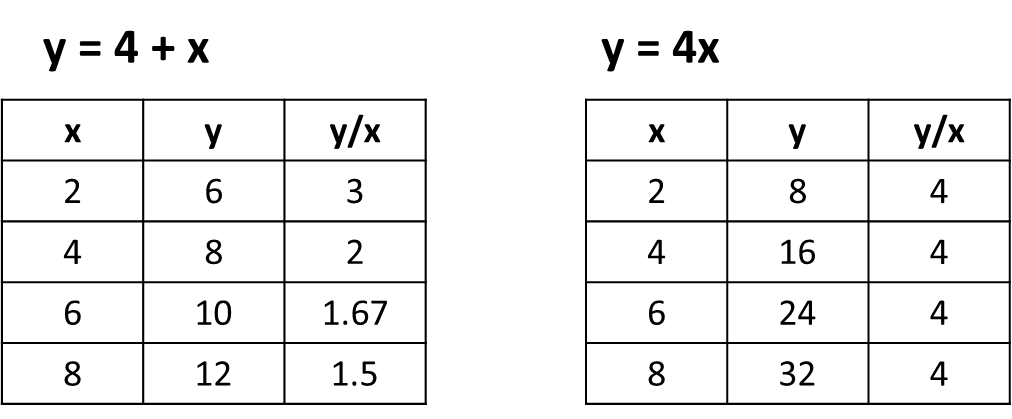
This tells us that the first case where the equation is y = 4 + x is not proportional! The values of y/x are not the same in any of the rations provided for x:y in this case. So, an additive relationship is not proportional - it is a non-proportional relationship (Remember how we discussed that a ratio is not an additive relationship?).

---

To begin with what ratios are, visit our other post: What do we mean by Ratio?

To understand the equivalent ratios, visit our other post: What are equivalent ratios and how exactly do we find them?

For double number line, visit our other post: Do we need double number line in ratio?

To understand proportional relationships, visit our other post: Ratio to proportional relationship: How do they connect?

To understand how to show proportional relationships using equations, visit our other post: Using Equation to express Proportional Relationship