Eduki

Look at the grid below. It has been filled in by different colors - purple and grey. 

These two colors make up the whole grid, so we can think of them as two parts of the whole grid. The ratio of purple to grey squares is 11:13. Because they are parts, this is also called a part-to-part ratio. If, however, you were to take the ratio of purple to all the squares, you would have 11:24. Here, purple is the part, and the total squares are the whole. So, this is a part-to-whole ratio. While such names are not necessarily that important, it helps us understand that ratio can be taken of any quantity, part, or whole.

Additionally, not all quantities need to be part of some whole. Two quantities that aren't parts of any whole can also be ratios. Like the ratio of someone's height and weight. 

Parts representing a general unit

“Parts” are also used for quantities of a ratio where the unit is the same, meaning as the general terms for unit when the units of all quantities involved in the ratio is the same. For example: Recipe for lemonade calls for 3 parts lemon juice with 2 parts water. The ‘parts’ could be spoons, cups, buckets, anything. Ratio will be the same as long as the parts described are the same. These parts make up the whole quantity.

We can use tape diagrams to understand this reasoning or can use other representations learned so far—discrete diagrams, number lines, or tables. 

Let’s look at a tape diagram for this. 

Let’s say that the following tape diagram shows the ratio of ducks to chickens in a farm. 

The first tape represents the number of ducks. It has 4 parts, so 4 ducks. The second tape represents the number of chickens with 5 parts, so 5 chickens. The ratio of ducks to chickens is 4:5. There are 9 parts in all, because 4 + 5 = 9.

Note that all the parts of the diagram that are the same size have the same value. Here, each part represents one duck or chicken. 

We can use this to find the parts when we know the total. Suppose we know there are 18 of these birds in the farm, and we want to know the number of ducks. We are told that the ratio is the same - the ratio of ducks to chickens is 4:5. 

The 9 equal parts on the diagram need to give us the 18 total birds. This means that each part will need to represent 2 ducks or chickens now. So, we just count the parts for ducks, which gives us 8 ducks in total. Using the same idea, we can see that the number of chickens is 10. In total, we need to get 18, 8 ducks and 10 chickens, which is what we got!

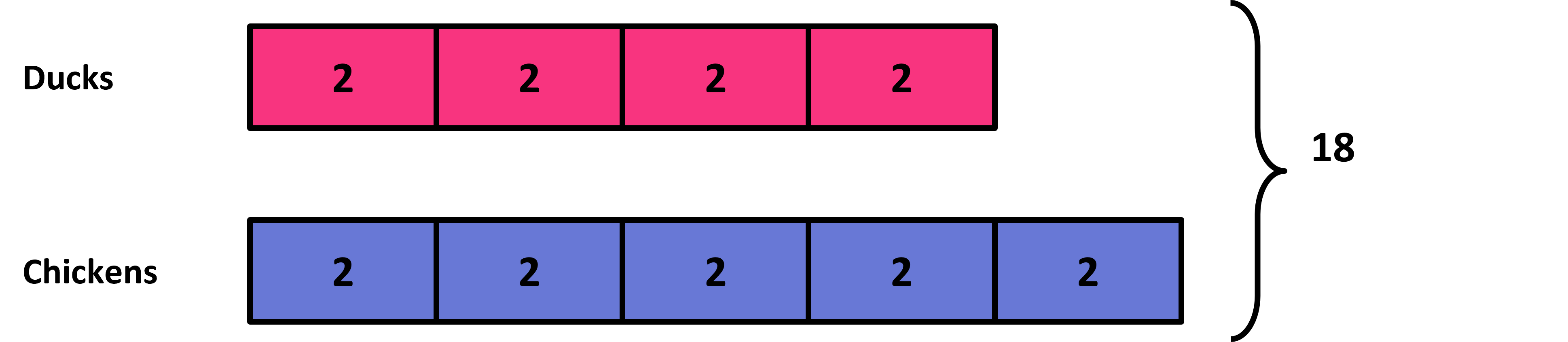
We could also do this numerically. We know that the ratio of ducks to total animals will be 4:9. The reason we use this part-to-whole ratio is because we are given the total number of birds, which is the whole. If the total is now 18, that means we need to multiply duck numbers by 2 as well to get 4 x 2 = 8 (because 9 x 2 = 18). 

To begin with what ratios are, visit our other post: What do we mean by Ratio?

To understand the equivalent ratios, visit our other post: What are equivalent ratios and how exactly do we find them?

For double number line, visit our other post: Do we need double number line in ratio?