Eduki

There is an alternative method of solving and understanding multiplication; multiplication as scaling. 

Let's take an example to understand this. We have a block of size 6 below. What does multiplying by 2/5 gives us? First, let's divide the block into 5 equal parts. Then the size of each part has to be 6/5 (since 6 ÷ 5 give 6/5 as the size of one part). Now we have the numerator 2 left. This means we need to take 2 of these parts, giving us 2 x 6/5 or 12/5. 

What we have done is first, dividing the quantity by denominator and finding the size of each part, then you multiply by the numerator to get the total number of such parts, thus giving us the answer. This method of understanding multiplication is helpful even when we multiply two fractions. The same process applies.

Furthermore, this method aligns with the idea of multiplication as scaling, rather than repeated addition, which is considered a better way to understand multiplication.  

We will look at the idea of scaling further with the three examples below. While the idea is the same as above, the process is slightly different. This also helps us estimate whether our new quantity is greater or less than the quantity that we operate on. 

There is a building measuring 10 m. You need to build a new building and are deciding the new height compared to the 10 m building. Can you tell which of the following options will give the the highest and smallest product (building height): 5/5 * 10, 3/5 *10 or 7/5*10? 

In all cases, the size 10 is being operated on.  

i. Finding 5/5 x 10: 

a. First, we 'scale down' 10 by 5. It is similar to dividing 10 into 5 parts and taking one part, but we simply decrease the size by 5. We see this below:

b. This new size is 10/5. We now have to 'scale up' by multiplying it by the numerator, 5. We can see this below:

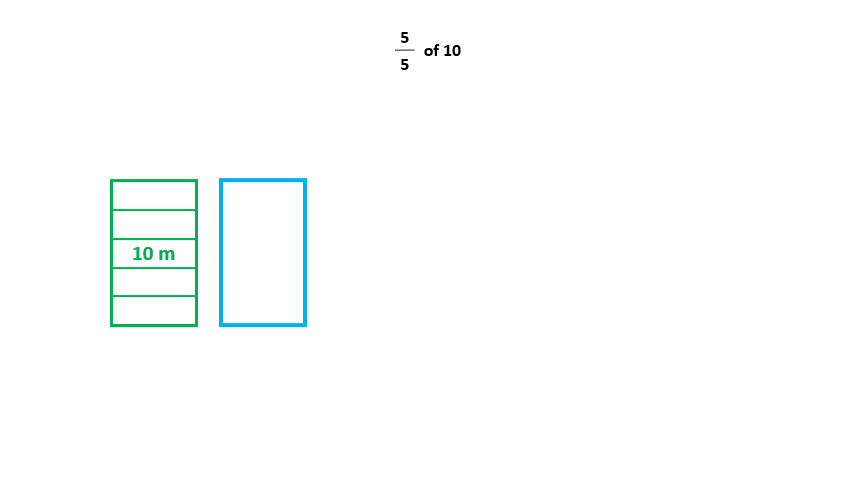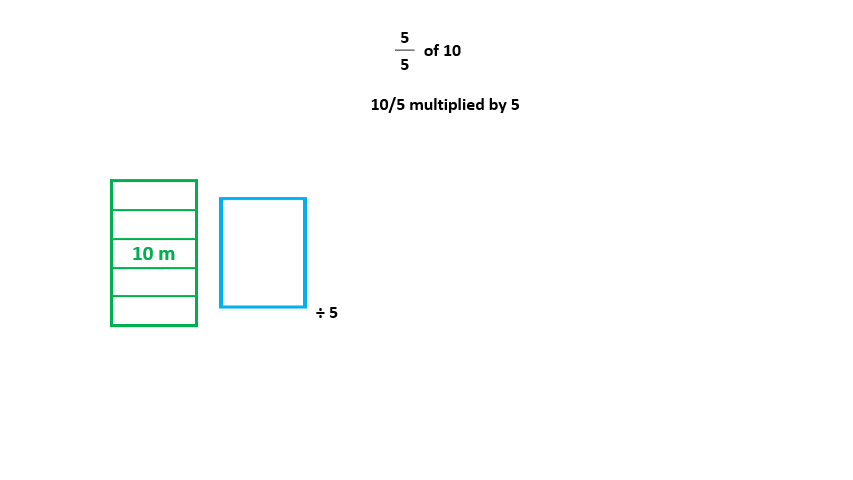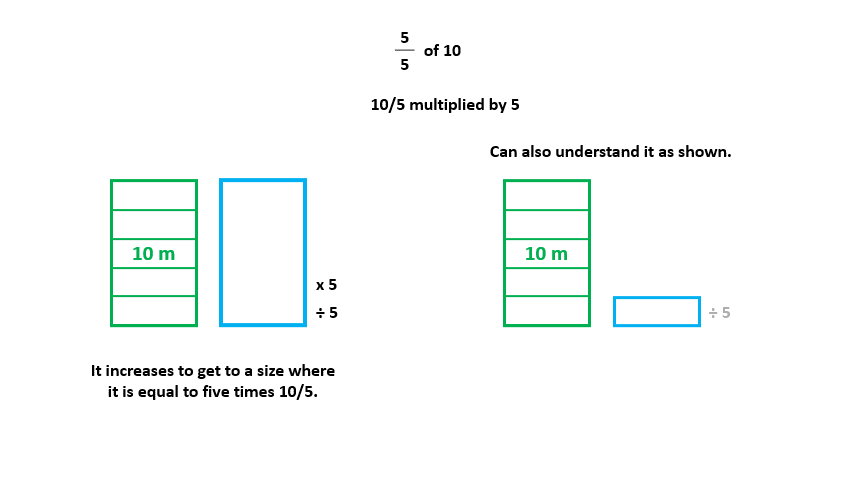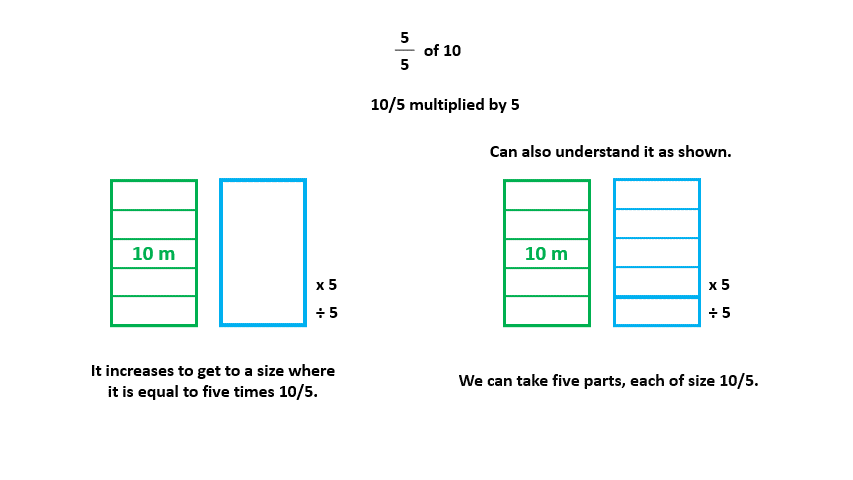
This gives us 10/5 x 5, which is equal to 50/5 = 10 This shows us that 10 is scaled down to 5 and then scaled up to 5, meaning there is no change. This makes sense because multiplying by 5/5 means multiplying by 1, which gives us the same number. 

This is also consistent with the idea of equivalence, where n/n x a/b = (nxa)/(nxb) = a/b. 

The same idea is applied to find the other two expressions as well: 

2. Finding 3/5 x 10:

First, we 'scale down' 10 by 5. It is similar to dividing 10 into 5 parts and taking one part, but here we simply decrease the size by 5. 

This new size is 10/5. We now have to 'scale up' by multiplying it by the numerator, 3. We can see the whole process below: 

We first have 10/5, which is then multiplied by 3, giving us 10/5 x 3 = 30/5 = 6.

You can check this using the multiplication method: 3/5 x 10 = 3x10/5 = 30/5 = 6. You get the same answer! In this case, we see that we first scale down by 5 but only scale up 3, which makes it obvious that the new quantity will be less than 10. 

We should already be familiar with the idea that multiplying any quantity by a fraction smaller than 1 gives a value smaller than the quantity (here, 10). So, the idea of scaling is consistent with this. Finally, do the same for 7/5 x 10. 3. First, we 'scale down' 10 by 5. It is similar to dividing 10 into 5 parts and taking one part, but here we simply decrease the size by 5. This new size is 10/5. We now have to 'scale up' by multiplying it by the numerator, 7. We can see the whole process below: 

We first have 10/5, which is then multiplied to 7, giving us 10/5 x 7 = 70/5 = 1.

In this case, it should be clear that the answer will be greater then 10 without any calculation. We first scale down by 5 but scale up 7, which makes it obvious that the new quantity will be more than 10. We should already be familiar with the idea that multiplying any quantity by a fraction greater than 1 gives a value greater than the quantity (here, 10). 

7/5 is an improper fraction greater than 1. So, the idea of scaling is consistent with this as well. Just like with whole numbers, fraction scaling works with fraction values as well.