Eduki

What is probability?

Let's consider two scenarios.

Andre and his dad have been fishing for 2 hours. In that time, they caught 9 bluegills and 1 yellow perch. The next time Andre gets a bite, what kind of fish do you think it will be? 

Have a look at the jar of marbles. If you are to close your eyes, shuffle the jar and pick one marble at random, what do you think will be its color?

In both of these questions, we have an intuitive idea of what is more likely to happen. We can get a feeling that the next time Andre gets a bike, it will be bluegill. Similarly, because there are many more green marbles than red, we’ll most likely pick the green one. 

In both cases, we analyze how likely the event will happen. Probability is the branch of mathematics that studies the likelihood that an event will occur. Unlike other branches of mathematics, probability deals with uncertainty. In real life, most things are uncertain. For example, it may or may not rain tomorrow. Our sales for this year may cross $80,000 or it could be less than that. Probability has risen in popularity in recent days as the world around us has become more complex and people need to make important decisions under uncertainty. 

Chance experiment, outcomes, and events

Have a look at the spinner. If you spin the wheel, the pointer will stop at one of the three colors - red, blue, or green. 

[spinner here]

Now, if I spin the spinner right now, what do you think will be the result?

Well, we don’t know what the result will be. Such an act of spinning a wheel is called a chance experiment. A chance experiment is a process of making an observation of something where the result is unknown. Each time a spinning wheel is spun, it’s a chance experiment. Similarly, each time a standard number cube is thrown or a coin is flipped, it is a chance experiment. This is because we cannot be certain of what will the result of this experiment be.

Each possible result of a chance experiment is called an outcome. For example, when you spin the wheel, one possible outcome is “blue”. So, this chance experiment has three possible outcomes - “blue”, “red” and “green”. The set of all possible outcomes is called a sample space. We say that the sample space is made up of the colors “blue” “green” and “red”. Spinning this spinner has a possible outcome of “red” but neither “yellow” nor “heads” is a possible outcome. 

Sometimes, we are interested in one particular outcome, and at other times we want to know about a set of outcomes. The set of one or more outcomes of interest is called an event. And we are interested in studying the likelihood of that event happening. In this sense, we can describe events using phrases such as “Impossible”,  “Unlikely”, “Equally likely as not”, “Likely”, “Certain” and so on.

In all the examples, we discussed, all of the outcomes are equally likely within each sample space. For example, it is equally likely for an outcome to be "green", "blue" or "red". Similarly, it is equally likely for an outcome to be "head" or "tail" when flipping a coin, and it is equally likely to get 1,2,3,4,5, or 6 when you roll a dice. However, it is not necessary that all possible outcomes must be equally likely. 

A random experiment 

A random experiment is a chance experiment where the outcomes are solely based on chance. 

When we spin the spinner, all three outcomes are equally likely. For this to be true, two things need to happen:

1. The red, blue, and green colored areas in the wheel area must be equal
2. Spinning the wheel must be a random experiment, i.e. the spinner does not favor any particular color. The experiment, for instance, would not be random if the spinner is crooked and thereby the pointer would land on “red” most of the time.

Here are some examples of random and non-random experiments.

Random experiment	Non-random experiment
	Something that is not random might be answering a multiple choice question on a test for a subject you've studied.
For example, if two people both want to read the same book, we could flip a coin to see who gets to read the book first.
An example is putting the integers 1 through 20 on a spinner with each number in an equal-sized section.

Measuring likelihood as a probability of an event

We established that in our spinner experiment, the likelihood of “blue”, “green” and “red'' is the same. Often, it is not enough to only know that the likelihood is equal or that the likelihood of one event is higher than the other. We want to have an actual numerical value rather than a vague sense of likelihood. To answer how probable something is to happen, we assign a probability.

The probability of an event is a measure of the likelihood that the event will occur. Probabilities are expressed using numbers from 0 to 1 and can be written as a fraction, decimal, or percentage. 

• If the probability is 0, that means the event is impossible. For example, when you flip a coin, the probability that it will turn into a bottle of ketchup is 0. The closer the probability of some event is to 0, the less likely it is.

• If the probability is 1, that means the event is certain. For example, when you flip a coin, the probability that it will land somewhere is 1. The closer the probability of some event is to 1, the more likely it is.

• Something that has a 50% chance of happening, like a coin landing heads up, can also be described by saying, “The probability of a coin landing heads up is 1/2.” or “The probability of the coin landing heads up is 0.5.”

When each outcome in the sample space is equally likely, we may calculate the probability of the desired event by dividing the number of outcomes for which the event occurs by the total number of outcomes in the sample space. 

So, in our spinner experiment, the size of the sample space is 3. The number of outcomes for the “blue” event is 1, so the probability of the event “blue” is ⅓ or 33.33%.

What does it mean by “equally likely” outcomes?

Students may think that the phrase "equally likely" means there is a 50% chance of it happening. Tell students that, in this context, each outcome is equally likely if the probability does not change if you change the question to a different outcome in the sample space. For example, "What is the probability you get a letter A from this bag?" has the same answer as the question, "What is the probability you get a letter B from this bag?"

Probability of an event with more than one outcome

Earlier, we worked with a spinner where all outcomes were equal. Now, let’s look at a slightly modified spinner. 

[spinners here]

What has changed? Well, the size of the sample space is 4 now. And the number of outcomes for the event “blue” is 2. So the probability of the event “blue” is now ½ or 50%.

Here, we are interested in the event "blue" and this blue is made up of two outcomes "a" and "b". There is a total of four outcomes, so the probability is given by 2/4 or 1/2. 

Let's look at another example. Suppose a bag contains 5 blocks. If we select a block at random from the bag, then the probability of getting any one of the blocks is 1/5. 

Now suppose a bag contains 5 blocks. Some of the blocks have a star, and some have a moon. If we select a block from the bag, then we will either get a star block or a moon block as an outcome. The probability of getting a star block depends on how many there are in the bag.

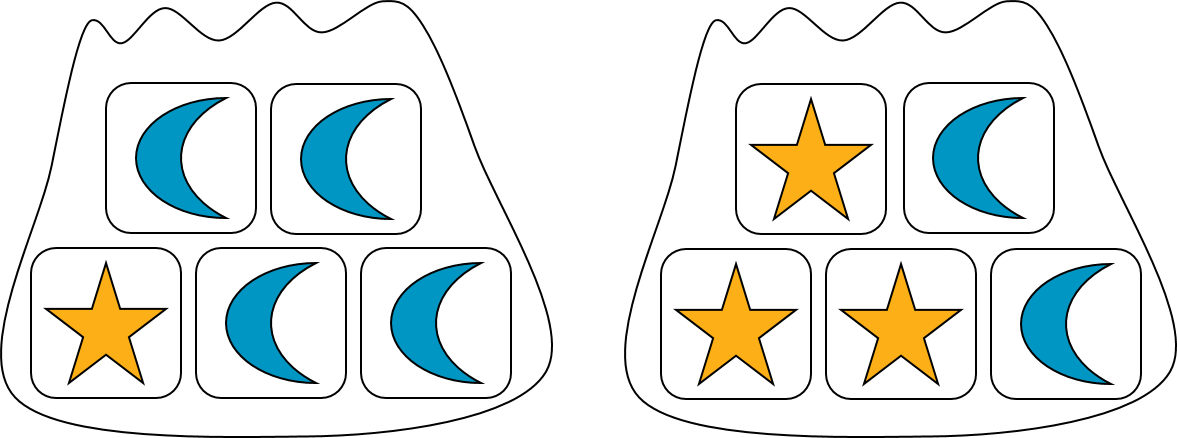
In this example, the probability of selecting a star block at random from the first bag is 1/5, because it contains only 1 star block. (The probability of getting a moon block is 4/5.) The probability of selecting a star block at random from the second bag is 3/5 because it contains 3 star blocks. (The probability of getting a moon block from this bag is 2/5.)

This shows that two experiments can have the same sample space, but different probabilities for each outcome.