Eduki

Whenever the expression in the equation is of px+q or p(x+q) form, then both the multiplicative and additive laws of quality have to be used. Both the forms can be transformed into each other and thus the laws can be used in any order. 

If we want to use the multiplicative law first, then we must transform the expression into the form of p(x+q) and if we want to use additive law first then we must transform the expression into px+q form. The process of transformation is done based on distributive law. Both laws have to be used in these kinds of expressions and using them in any order will give us the same answer. However, sometimes one law may be suitable more than the other. 

If a pizza delivery company charges 8 dollars per pizza and 2 dollars fixed charge for delivering any number of pizzas, then the total bill will be equal to 2 more than 8 times the number of pizzas. It can be written in the form of an expression as 8𝑥+2 where x is the number of pizzas. If the bill for a certain order on Tuesday is worth 74 dollars then how many pizzas must have been ordered?

The solution to this question is pretty simple. It is asking us what number multiplied by 8 and increased by 2 becomes 74. 

Or 8𝑥+2= 74

There is a fixed algorithm for solving these types of problems. Firstly the part added in the expression is eliminated using the additive law of equality.

Or 8𝑥+2-2=74-2

Or 8𝑥=72

Then later the multiplicative law of equality is used to divide both sides of the equation using a factor so that only the variable remains on one side other side giving us a constant number.

Here that factor is 8

or 8𝑥/8=72/8

or 𝑥=9 

However, if the problem was with the form 

8(𝑥+2)=72

Then there are two ways; 

One way is to use the distributive property and transform it into an earlier type in which the additive property of equality is used first followed by the multiplicative property of equality. 

Another way is to make the equation as it is and use the multiplicative law of equality

[8(𝑥+2)]/8=72/8

or (𝑥+2)=9

Then use the additive property of equality 

𝑥+2-2=9-2

or 𝑥=7

 

Hanger diagrams

Equations can be represented in the form of hanger diagrams that are similar to that of beam balance. It has two arms extending from the suspension point and generally gives the idea of which side is heavier among the two. The two sides are basically the quantity that is located on either side of the equal to sign. If the top bar (with two arms) is completely horizontal, then the two quantities are known to be equal. If the bar isn't horizontal, then one of the sides is heavier, or quantities on one of the sides are more than the other. 

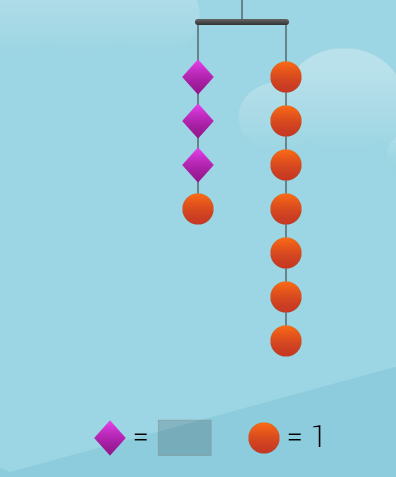
The hanger diagram can be used as a medium to solve any equation. The hanger diagram given above is of equation 3𝑥+1=7. 

Firstly the index at the bottom of the diagram states that the value of the diamond is unknown while each circle has 1 unit. First, the unknown entity is isolated on only one side and the remaining on the other side. If the unknown quantity is present on both sides, then an equal number of unknown quantities is deducted from both sides. It is the use of the additive law of equality. 

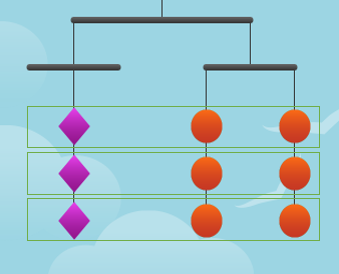
Here one circle is present on the left-hand side which is less than seven circles on the right-hand side. One circle is deleted from both sides to get three diamonds on the left-hand side and six circles on the right-hand side. 

Then the unknown and known quantities separated on the two sides are grouped in a way as given below. 

That shows that a diamond is equal to the quantity of two circles. Since a circle is 1 unit, the diamond has to be of 2 units.