Eduki

A minimum of three sides are required to create a closed figure. A figure with three sides has three angles inside it. A closed figure formed with straight sides only is known as a polygon. In that sense, a triangle is the simplest polygon available. If the polygon has all of its sides equal to each other, then it is known as a regular polygon. A polygon has all of its angles equal to each other. The three angles of a triangle when added are equal to 180 degrees. 

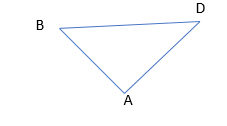
Suppose we have a triangle BAD as shown in the figure. 

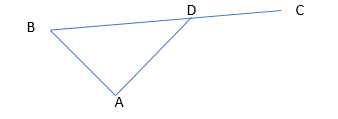
Then according to recent learnings, the angles formed at the three vertices; A, B, and D are summed to get 180 degrees. Let's produce the line and extend it to C. 

Then there are two angles formed at point D, One is ∠ADC and the other is ∠ADB. Since these both also sum to give 180 degrees because of both the angles being formed in a straight line. 

 ∠ADC +  ∠ADB =180

and (∠ABD + ∠BAD) + ∠ADB = 180

When we compare the two equations, we get, 

 ∠ADC= ∠ABD + ∠BAD

This can be translated into a theorem that says that the exterior angle of a triangle is equal to the sum of two opposite interior angles.

If all the angles in a triangle are less than 90 degrees, then the triangle is known as an acute-angled triangle.

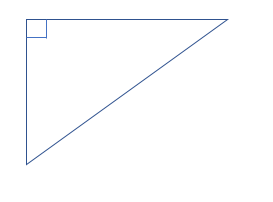
If one of the angles in a triangle is 90 degrees, then the triangle is known as a right-angled triangle.

If any of the angles in a triangle is more than 90 then the triangle is an obtuse angled triangle. 

Triangles are of three types according to the equality of sides.

If none of the sides are equal to each other then the triangle is known as a scalene triangle, None of the angles are equal in such triangles.

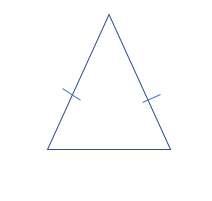
If two of the sides are equal, then such triangles are known as an isosceles triangles. The two angles opposite to the equal sides are equal in such triangles. 

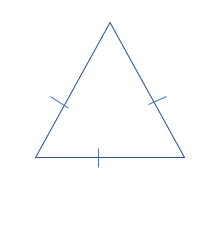
If all three sides are equal, then each of the internal angles is equal to the other, and such a triangle is known as an equilateral triangle. 

Internal angle of other polygons

A polygon with 4 sides is a quadrilateral. Based on different relations and specialties among the dimensions of the quadrilateral, it is of different types. 

As we already learned that the angle value used for a full circle angle is 360 degrees, we can see if a particular number of regular polygons can be rotated to overlap the full circle so that we can find out what is the value of the internal angle of the polygon. For example, equilateral triangles can overlap 360 degrees like this.