Eduki

Spheres

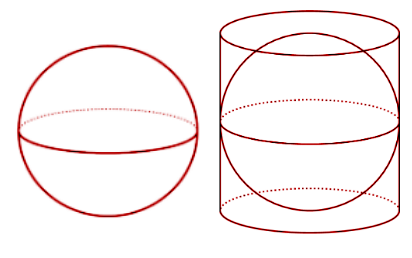
Another type of curved surface object is a sphere that does not have any flat face at all. The surface area of the sphere is measured with the help of a cylinder of the same dimensions as the sphere. 

 

 

When a hollow cylinder with the same radius of the sphere and height equal to the diameter of the sphere is taken and the sphere is inserted into a flexible cylinder. It is found that the cylinder completely covers the upper and lower surfaces of the sphere. That means that the lateral surface area of the cylinder and the sphere are the same. 

Total surface area of the cylinder= 2πrh=2πr*2r=4πr2

That is the total surface area of the sphere.

 

To find the volume, a cone of the same height and radius as the cylinder is filled with liquid. When the liquid is poured into the setting, it completely fills the gap between the sphere and the cylinder. That means that the volume of the cone and sphere when added together gives the volume of the cylinder. 

Volume of cone + Volume of sphere= Volume of cylinder

Or, Volume of sphere=Volume of cylinder-Volume of cone

=π*r2*h-(⅓)π*r2*h

=(⅔)π*r2*h

But we know h=2r

=(4/3)π*r3

Hemisphere

Half a sphere or the shape that we get when we cut the ball in half is a hemisphere and so it has a volume exactly half of the sphere

 

 

Volume of hemisphere =[(4/3)π*r3]/2=(2/3)π*r3

Talking about the area, one more surface that is circular is introduced while cutting the sphere. So it is found that the lateral surface area of the hemisphere is equal to half of the total surface area of the sphere

Lateral surface area of the hemisphere= total surface area of sphere/2

=(4πr2)/2

=2πr2

Total surface area of the hemisphere= lateral surface area of hemisphere area of base circle

=2πr2+πr2

=3πr2